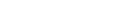Research555
Neutrinos and the Standard Model
The Standard Model of particle physics is based on the idea that there are three distinct kinds of sub-atomic particles: (1) fundamental fermions like quarks, electrons, and neutrinos, (2) gauge bosons like the photons, gluons, W, and Z particles that are responsible for forces between particles, and (3) a complex scaler particle like the Higgs that interacts with particles to give them mass. The particles form a sort of "periodic table" similar to the chemical elements, as shown here. The fundamental fermions are classified as quarks (purple) or leptons (green) depending on whether or not they interact with gluons (g) via the Strong Force. The quarks do interact with gluons, and therefore make up the protons and neutrons that are inside atomic nuclei. The leptons (like the electron) only interact electrically via the photon (γ) or weakly via the Z or W. This is why electrons are outside the nucleus to make the atoms of the matter we are familiar with – they just don't interact strongly enough to keep them penned up!
Neutrinos (ν) have no electric charge and thus only interact weekly with other particles. So weakly, in fact, that neutrinos from the sun pass right through the earth and allow specially designed neutrino detectors to image the sun when it is below the horizon!
Like the quarks, neutrinos come in three types called flavors. For neutrinos, the names of the flavors are e μ and τ based on the association of the flavor with one of the charged leptons: electron (e), muon (μ), and tauon (τ).
Are Neutrinos Fundamentally Different?
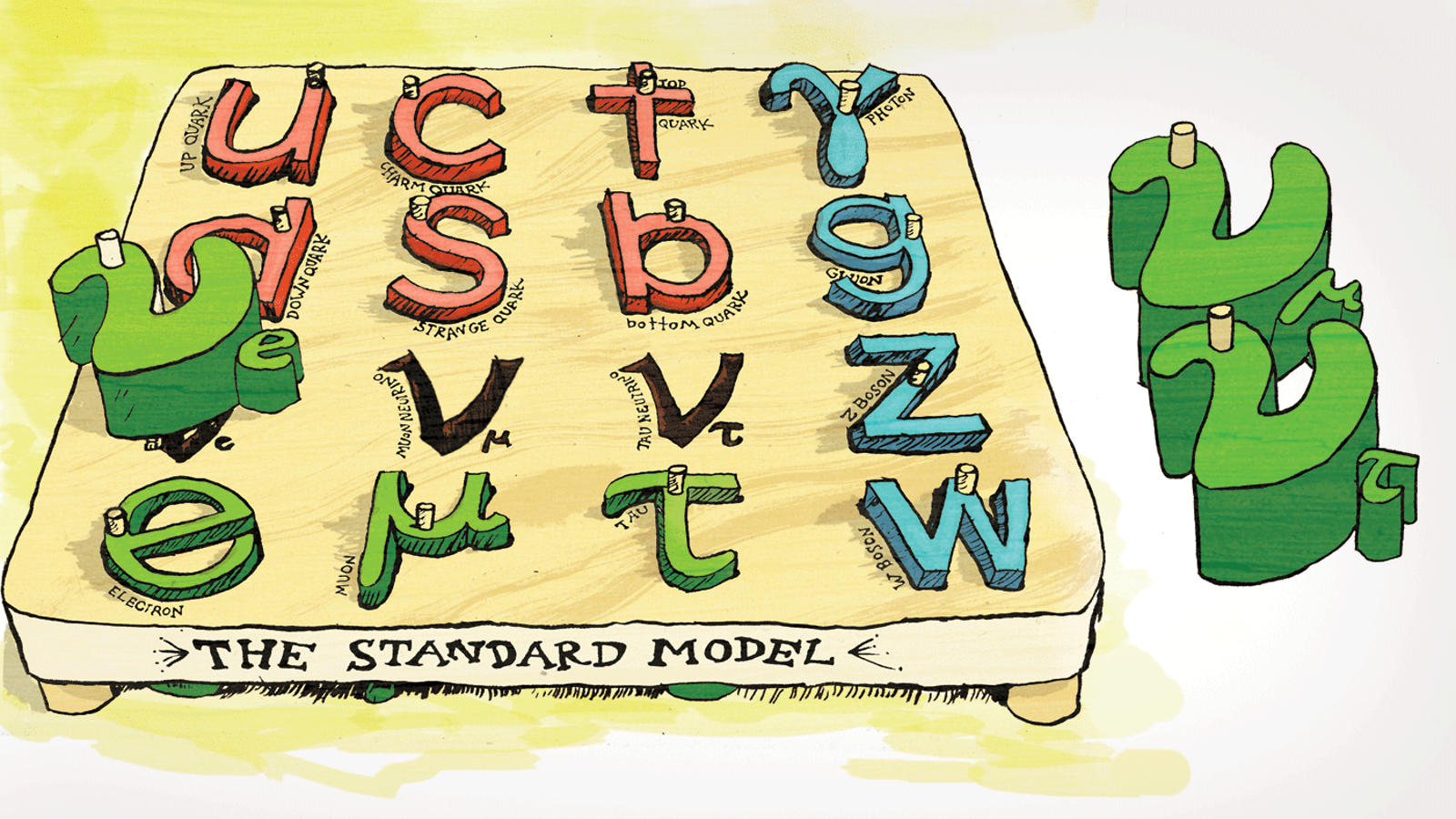
The Lagrangian for the Standard Model Electroweak sector is given by the equation on the right, which is composed of a kinetic energy term and two gauge fields: (1) a U(1)Y field with coupling constant g', and (2) an SU(2)L gauge field with coupling g.
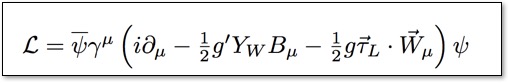
After symmetry breaking the four gauge field bosons implied by these field mix to form our friends the photon (γ), Z, and W±. Looking at the explicit Lagrangian after symmetry breaking, we get a part that corresponds to W exchange (Charged Current - or CC) and Z or γ exchange (Neutral Current - or NC, in which I have also included the E&M terms).
The Lagrangian for the Standard Model Electroweak sector is given by the equation on the right, which is composed of a kinetic energy term and two gauge fields: (1) a U(1)Y field with coupling constant g', and (2) an SU(2)L gauge field with coupling g. After symmetry breaking the four gauge field bosons implied by these field mix to form our friends the photon (γ), Z, and W±. Looking at the explicit Lagrangian after symmetry breaking, we get a part that corresponds to W exchange (Charged Current - or CC) and Z or γ exchange (Neutral Current - or NC, in which I have also included the E&M terms). Here I have written only the first family fermions, up (u), down (d), electron neutrino (ν), and electron (e). The (1-γ5)/2 operator picks out the "left handed chirality" of the wavefunctions for these particles. Chirality is a sort of relativistic direction of spin. Strange to say, nature prefers that charged current interactions happen only with left handed chirality!
The J variables stand for currents:
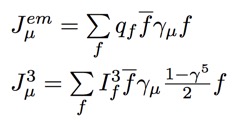where the top current is the electromagnetic one, with familiar coupling constant q, and the bottom one if the weak isospin current, with the coupling constant I3 (third component of weak isospin). Thus each fundamental fermion in our 'periodic table" is described by these two simple quantum numbers! Historically, we usually write YW instead of q, where YW is hypercharge, given by:
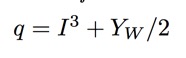
The table below shows the quantum numbers for the first generation of leptons (electons and neutrinos), where the bar above the particle indicates the anti-particle. The subscript L or R indicates the chirality of the particle. Note the nice symmetry of these numbers (one reason for using Y instead of q), but also note the strange result: right chiral (R) antineutrinos would have I=0 and YW=0, so they have no electromagnetic or weak interactions at all - they are "sterile."
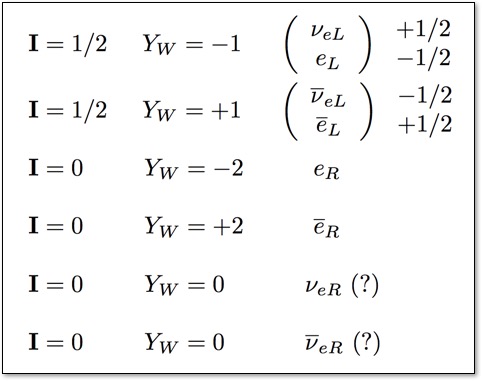
Neutrino Oscillations
CP Violation
Majorana Neutrinos
Supernova Neutrinos
Diffuse Supernova Neutrinos
Baryon Number Violation
