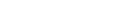Majorana555
The Dirac Equation in one dimension for a free spin 1/2 fermion is given by the equation below.
The first term can be viewed as a "kinetic energy" term while the second is a "mass" term. The solutions are 4-component "spinors". Four components are needed to represent "spin up" and "spin down" matter and antimatter particles. This equation can be derived using the Euler-Largrange equation and the Lagrangian given by the equation below, where the spinor with the bar is the conjugate spinor defined by the Hermitian conjugate of the spinor multiplied from the right by γ0.
In the Standard Model this is called the "Dirac mass term" and is thought of as the result of interactions with the Higgs boson as the fermion propagates through space.
For neutrinos, if we represent the spinor as ν then the Dirac mass term can be written separately, and broken down into the relativistically invariant version of "spin up/down" called right (R) or left (L) "chirality", as shown below.
The mD Dirac mass is then related to the Higgs by a coupling constant (y) and a Higgs vacuum expectation value (v). The Higgs then links "Left" and "Right" chiral parts of the propagating fermion, which behaves as a mass, rather like the refractive index of a transparent material apparently slows down light. This Standard Model view all fits together very well, but is it true for neutrinos?
It turns our that because neutrinos have no electric charge, there is another solution to the Dirac equation that does not have the 4-component spinors as shown above. Proposed in 1937 by Ettore Majorana, this solution is written as shown the left, with only left chiral spinors and their conjugate. This means there are only two neutrino states, not four as shown below.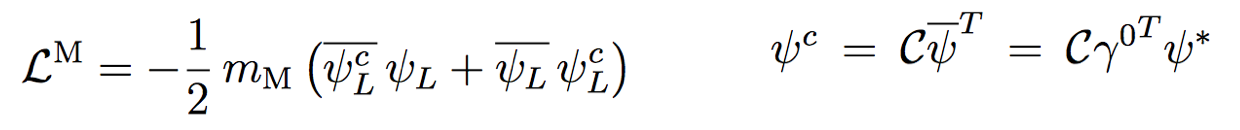 
In other words, neutrinos would not exhibit matter/antimatter symmetry, but rather would be their own antiparticle!
Of course, there is nothing to prevent neutrinos from having both Dirac and Majorana mass terms. In fact, this leads to a possible explanation for the smallness of the neutrino mass called the "seesaw mechanism."
